
EHM model
Crystal is considered as a chain of the undeformable molecules, which are connected with each other by the elastic hinges with elastic constant f .

The chain is compressed by the force p along its axis. The vertical springs make elastic support for the nodes of the chain. un denotes the transversal displacement of nth node.
The Hamiltonian of the crystal may be written in the dimensionless form:
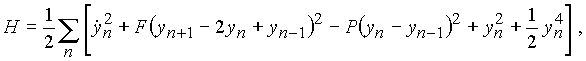
where the first term is the kinetic energy, the second one is the potential energy of the elastic hinge, the third one is the work done by the external force and the last two terms give the energy of the elastic nonlinear support due to the vertical springs.
Equation of motion for nth hinge has the form
![]()
The role of the elastic hinges is to keep the chain as a straight line while the compression force plays a destructive role, it tends to destroy the horizontal arrangement of bars. The competition between these two factors, F and P, gives rise to modulation instability in the model.
N-periodic and Interpenetrating Soliton Structures of EHM Model
Obviously, equation of motion has a trivial solution un=0. A few types of N-periodic solutions, for which yn=yn+N, can be found.
The solution with the period N=2 has the form
![]()
![]()
where sign "+" corresponds to the structure with even nodes up and odd ones down and sing "-" vice versa. This solutions exists if P>4F+1/4.
Two interpenetrating kinks describe a smooth conjugation of the "+" and "-" structures:
![]()
Red and blue lines are drawn for better visualization. Consideration of two slowly varying functions for modeling of the displacements in the system makes it possible to develop generalized continuum model (2-field continuum).
If the two-periodic transversal force Qn=(-1)nq is applied to the nodes of the EHM-system, there are two locally stable zigzag structures with different energies. One can load .avi-file (132Kb)
, witch represent the autosoliton, which transforms the structure with a large energy into the structure with a small energy in system with dissipation. The autosoliton has the form of two moving interpenetrating kinks.The solution with the period N=3 has the form
![]()
![]()
![]()
This solutions exists if P>3F+1/3. Again, we have "+" and "-" structures:
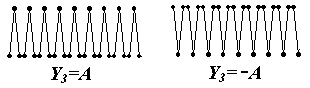
The 3-field soliton conjugates these structures
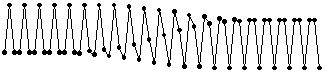
or in animated form
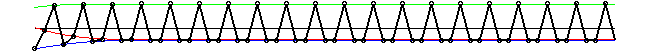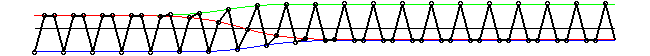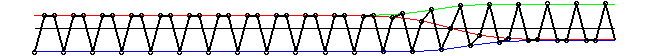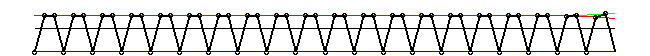
The "+" and "-" four-periodic solutions are
![]()
![]()
and the 4-field soliton is given in Figure:

Autowaves in the EHM model. The solitons become unstable at certain magnitudes of the parameters f and p. Then it generates the two autowaves propagating in the opposite directions. The autowaves transform the metastable four-periodic structure into a four-periodic structure modulated with a long wave. We introduced a strong viscous friction in the system but the autowaves move with the constant velocity. The moving force comes from the energy delivered in the course of structure transformation (domino effect).
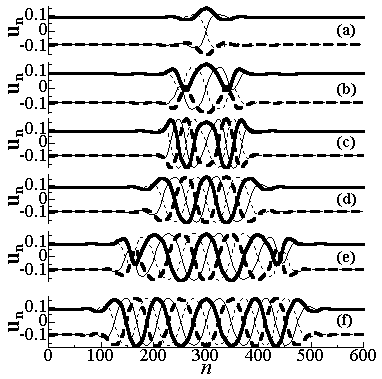
The time evolution of the unstable 4-field soliton in the four-periodic structure. The four lines of different style go through the particles with numbers 4n, 4n+1, 4n+2, and 4n+3.
|
For further information see the references. |