The dynamics of Josephson junction is given by the nonlinear differential equation

which is the equation for the forced damped driven pendulum (Ref. [1]). This analogy is used for graphic presentations.

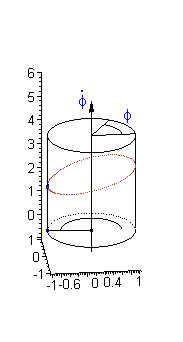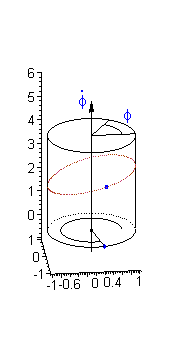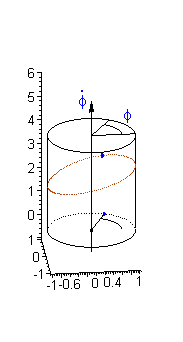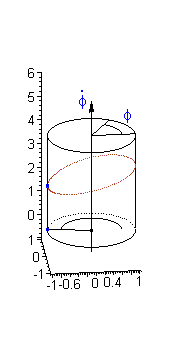
Since the unknown variable appears under sine function it is convenient to take a cylinder phase space.

It is important to note, that in cylindrical phase space there are two kinds of closed paths:

a) Closed paths of the first kind encircling an equilibrium point. In term of the mechanical analog this type of trajectory corresponds to an oscillatory motion of the pendulum.

b) Closed paths of the second kind (see above) go around the cylinder without encircling an equilibrium point. In term of the mechanical analog this type of trajectory corresponds to a rotary motion of the pendulum.

For discrete nonlinear system into environment the closed paths of the first kind lead to the discrete breathers (DB). The closed paths of the second kind lead to the rotobreathers (RB).

For junction and damped pendulum there is only closed path of the second kind.

The system of equations for Josephson ladder are

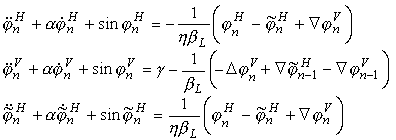
where

These equations are used for investigations of the rotobreather structures. There are different methods for obtaining of RB(DB) solutions in discrete nonlinear systems. One of the methods is realized in MapleVR5 code (JL.wms) and presented at the MapleV worksheet. The realized method, parameters and results are described in Ref. [2]. Experimental results are given, for example, in Ref. [3, 4].

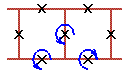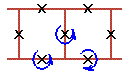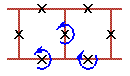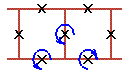
Two cell rotobreathers in Josephson ladder are presented here:

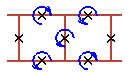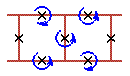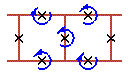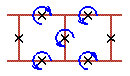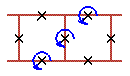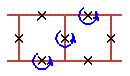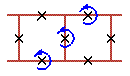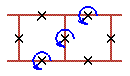To see rotobreather dynamics and representation within the framework of pendulum analogy click on the picture [up-down symmetry S_ud (Fig. 1), inversion symmetry S_in (Fig. 2), left-right symmetry S_lr (Fig. 3), no symmetry (Fig. 4)].

An examples of three cell rotobreather structures in Josephson ladder are given here

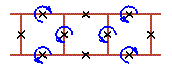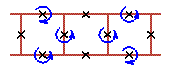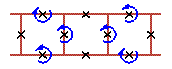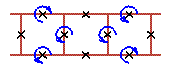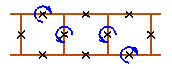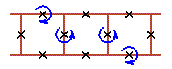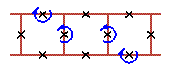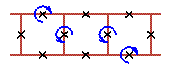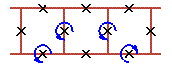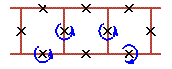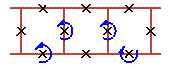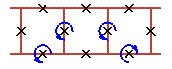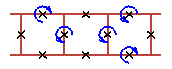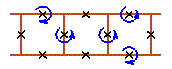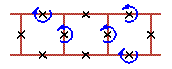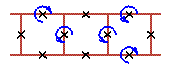To see rotobreathers (Fig. 5, Fig. 6, Fig. 7, Fig. 8) click on the picture.

Many cell rotobreather structures can be derived too. To see some of them click here: many cell rotobreathers.

References

1. A.Barone and G.Paterno Physics and applications of the Josephson effects. Wiley, New York, 1982.
2. S.Flach and M.Spicci Rotobreather dynamics in underdamped Josephson junction ladders. J. Phys. Cond. Matter 11 (1999) 321-334.
3. E.Trias, J.J.Mazo, T.P.Orlando Discrete breathers in nonlinear lattices: Experimental detection in a Josephson array. Phys. Rev. Lett. 84, 741 (2000).
4. P. Binder, D. Abraimov, and A.V. Ustinov Diversity of discrete breathers observed in a Josephson ladder. Phys. Rev. E 62, 2858 (2000).

• A.Ustinov GROUP (Physikalisches Institut III, Universitat Erlangen-Nurnberg)
• Theory and Simulation of Complex Systems (Condensed Matter Physics Department, University of Zaragoza)
• Sergej Flach's Discrete Breather Homepage  Reprints (Max-Planck-Institut für Physik komplexer Systeme, Dresden)
• LOCNET: Localisation by Nonlinearity and Spatial Discreteness, and Energy Transfer, in Crystals, Biomolecules and Josephson Arrays

   =================================

• A.E. Miroshnichenko, S. Flach, M. V. Fistul, Y. Zolotaryuk, J.B. Page Breather in Josephson junction ladders: resonances and electromagnetic waves spectroscopy. Phys. Rev. E 64, 066601 (2001). [ cond-mat//0103280 ]
• M. V. Fistul, A.E. Miroshnichenko, S. Flach, M.Schuster, A.V.Ustinov Incommensurate dynamics of resonant breathers in Josephson junction ladders Phys. Rev. B 65, 174524 (2002). [ cond-mat/0111460 ]

   =================================

Thank you for visiting this page. You are very welcome to contribute ideas for improvements. Let me know what you think.  Andrey

Link: Web Site Solitons and Soliton Collisions (Tver State University).