Динамика джозефсоновских контактов моделируется нелинейным дифференциальным уравнением

которое является также уравнением нагруженного маятника в вязкой среде [1]. Эта аналогия используется для графических представлений.

Поскольку неизвестная функция появляется в синус функции, полезно использовать для представлений цилиндрическое фазовое пространство.

Важно отметить, что в цилиндрическом фазовом пространстве существует два типа замкнутых фазовых траекторий:

a) Замкнутые траектории первого рода огибают положение равновесия. В терминах механической аналогии этот тип траектории соответствует колебательному движению маятника.

b) Замкнутые траектории второго рода расположены на цилиндре, не огибая положения равновесия. В терминах механической аналогии этот тип траекторий соответствует вращательному движению маятника.

Для дискретных нелинейных систем, находящихся в некоторой среде, замкнутые циклические траектории первого рода приводят к дискретным бризерам. Замкнутые траектории второго рода - к ротобризерам.

Для контактов и маятников в вязкой среде есть только замкнутые траектории второго рода.

Система уравнений для JL имеет вид

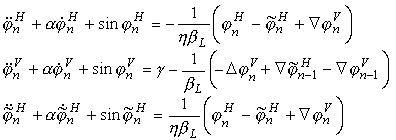
Эти уравнения используются для исследований ротобризерных структур. Есть различные методы нахождения рото-бризеров и дискретных бризеров в дискретных нелинейных системах. Один из методов реализован в MapleVR5 программе JL.wms и представлен на MapleV рабочей страничке. Реализованный метод, параметры и результаты описаны в [2]. Экспериментальные результаты представлены, например, в [3, 4].

Двух-ячеечные ротобризеры представлены ниже:

Чтобы посмотреть динамику и представление в рамках маятниковой аналогии стукните по картинке. Ротобризеры с различной симметрией S_ud (Fig. 1), S_in (Fig. 2), S_lr (Fig. 3), отсутствие симметрии (Fig. 4).

Примеры трех-ячеечных ротобризерных структур приведены ниже

Чтобы посмотреть ротобризеры (Fig. 5, Fig. 6, Fig. 7, Fig. 8), стукните по картинке.

Многоячеечные ротобризерные структуры могут быть получены также. Посмотреть некоторые из них можно здесь: многоячеечные ротобризеры.

1. A.Barone and G.Paterno Physics and applications of the Josephson effects. Wiley, New York, 1982.
2. S.Flach and M.Spicci Rotobreather dynamics in underdamped Josephson junction ladders. J. Phys. Cond. Matter 11 (1999) 321-334.
3. E.Trias, J.J.Mazo, T.P.Orlando Discrete breathers in nonlinear lattices: Experimental detection in a Josephson array. Phys. Rev. Lett. 84, 741 (2000).
4. P. Binder, D. Abraimov, and A.V. Ustinov Diversity of discrete breathers observed in a Josephson ladder. Phys. Rev. E 62, 2858 (2000).

Ссылки:

• A.Ustinov GROUP (Physikalisches Institut III, Universitat Erlangen-Nurnberg)
• Theory and Simulation of Complex Systems (Condensed Matter Physics Department, University of Zaragoza)
• Sergej Flach's Discrete Breather Homepage Reprints (Max-Planck-Institut für Physik komplexer Systeme, Dresden)
• LOCNET: Localisation by Nonlinearity and Spatial Discreteness, and Energy Transfer, in Crystals, Biomolecules and Josephson Arrays

   =================================

• A.E. Miroshnichenko, S. Flach, M. V. Fistul, Y. Zolotaryuk, J.B. Page Breather in Josephson junction ladders: resonances and electromagnetic waves spectroscopy. Phys. Rev. E 64, 066601 (2001). [ cond-mat//0103280 ]
• M. V. Fistul, A.E. Miroshnichenko, S. Flach, M.Schuster, A.V.Ustinov Incommensurate dynamics of resonant breathers in Josephson junction ladders Phys. Rev. B 65, 174524 (2002). [ cond-mat/0111460 ]

   =================================

Спасибо за посещение странички. Сообщите, что Вы думаете.   Андрей

Сайт: Солтоны. Столкновения и взаимодействия солитонов.