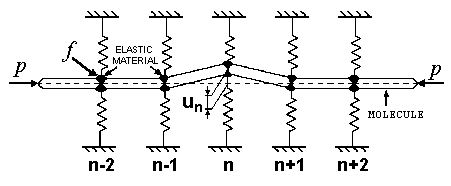
Упруго-шарнирная модель (EHM model)
Кристалл рассматривается как цепочка недеформируемых молекул, которые связаны друг с другом упругими шарнирами с константой упругости f .

Цепь сжата вдоль ее оси с силой p. Вертикальные пружины осуществляют упругое закрепление в узлах цепочки. un обозначают поперечные смещения n-го узла.
Гамильтониан кристалла может быть записан в безразмерной форме:
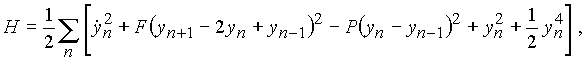
где первый член - кинетическая энергия, второй - потенциальная энергия упругих шарниров, третий - работа внешних сил, а последние два члена дают энергию упругой нелинейной заделки вертикальных пружин.
Уравнения движения для n-го шарнира имеют вид
![]()
Роль упругих шарниров - держать цепочку как прямую линию, в то время как сжимающая сила играет деструктивную роль. Она стремится разрушить горизонтальное положение стержней. Борьба между этими двумя факторами, F и P, дает путь неустойчивости в модели.
N-перодические и взаимопроникающие солитонные структуры упруго-шарнирной модели
Очевидно, что уравнение движения имеет тривиальное решение un=0. Несколько типов N-периодических решений, для которых yn=yn+N, могут быть найдены.
Решение с периодом N=2 имеет вид
![]()
![]()
где знак "+" соответствует структуре с четными узлами вверху и нечетными внизу, а при знаке "-" наоборот. Это решение существует, если P>4F+1/4.
Два взаимопроникающих кинка описывают плавное соединение "+" и "-" структур:
![]()
Красная и голубая линии нарисованы для лучшей визуализации. Введение двух плавно-изменяющихся функций для моделирования смещений в системе делают возможной разработку обобщенной континуальной модели (2-полевой континуум).
Если двух-периодическая поперечная сила Qn=(-1)nq приложена в узлах упруго-шарнирной системы, то существуют две локально-устойчивые зиг-заг структуры с разными энергиями. Можно загрузить .avi-файл (132Kb)
, который представляет автосолитон, который трансформирует структуру с большой энергией в структуры с меньшей энергией в системе с диссипацией. Автосолитон имеет форму двух движущихся взаимопроникающих кинков.Решения с периодом N=3 имеют форму
![]()
![]()
![]()
Это решение существует, если P>3F+1/3. Опять мы имеем "+" и "-" структуры:
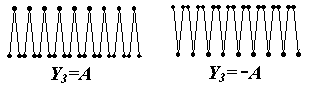
3-полевое решение описывает эти структуры
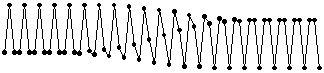
или в анимационной форме
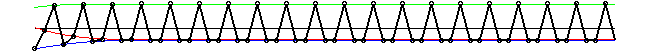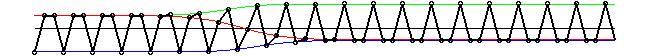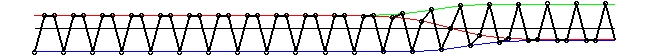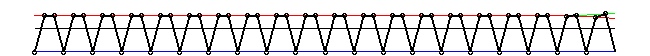
Четырех-периодические "+" и "-" решения
![]()
![]()
и 4-полевой солитон дан на рисунке:

Автоволны в упруго-шарнирной модели. Солитоны становятся неустойчивы для определенных значений параметров f и p. Генерируется две автоволны распространяющихся в противоположных направлениях. Автоволны преобразуют мета-устойчивую четырех-периодическую структуру в четырех-периодическую структуру описываемую длинной волной. Мы вводим вязкое трение в систему и автоволна движется с постоянной скоростью. Движущая сила возникает от структурного перехода (эффект домино).
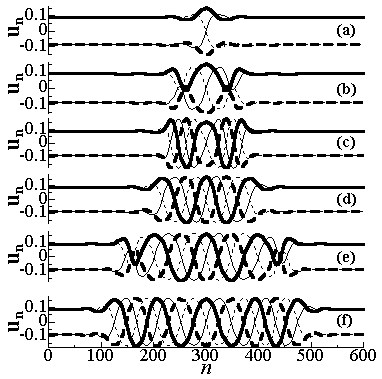
Эволюция во времени неустойчивого 4-полевого солитона в 4-периодической структуре. Четыре линии различного стиля проходят через частицы с номерами 4n, 4n+1, 4n+2 и 4n+3.
|
Для дополнительной информации можно посмотреть статьи. |