Sine-Gordon Solitons and Soliton Collisions:
Pendulum Model
by
Andrey E. Miroshnichenko
, andrey.miroshnichenko@anu.edu.au,
Aleksey A. Vasiliev
, aleksey.vasiliev@tversu.ru,
Sergey V. Dmitriev
, sergey@iis.u-tokyo.ac.jp
NOTE:
In the present worksheet, with the help of Maple, we apply the Backlund transformation for derivation of multi-soliton solutions to the sine-Gordon equation. The solutions are visualized for the system of coupled pendulums, having the sine-Gordon equation as the continuous analog.
Introduction
We consider the linear chain of N pendulums each coupled to the nearest neighbors by the elastic bonds. Let us denote the angle of rotation of
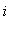 -th pendulum by
-th pendulum by
![phi[i]](images/SOLPEN2.gif) and the angle velocity by
and the angle velocity by
![omega[i]](images/SOLPEN3.gif) . Each pendulum experiences the angular moment due to the gravity and the angular moments from the two elastic bonds, which are proportional to the difference in angles of rotation of the coupled pendulums with the coefficient
. Each pendulum experiences the angular moment due to the gravity and the angular moments from the two elastic bonds, which are proportional to the difference in angles of rotation of the coupled pendulums with the coefficient
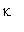 . Under the assumption that all pendulums have the same moment of inertia, J, the set of equations of motion takes the form Ref. [1]
. Under the assumption that all pendulums have the same moment of inertia, J, the set of equations of motion takes the form Ref. [1]
| > |
J*diff(omega[i](t),t)=Gamma1[i]+Gamma2[i];
|
,t) = Gamma1[i]+Gamma2[i]](images/SOLPEN5.gif)
where
![Gamma1[i]](images/SOLPEN6.gif) is the angular moments from the elastic bonds and
is the angular moments from the elastic bonds and
![Gamma2[i]](images/SOLPEN7.gif) is the gravity angular moment.
is the gravity angular moment.
The angular moments from the left and right elastic bonds are
![kappa*(phi[i-1]-phi[i])](images/SOLPEN8.gif) and
and
![kappa*(phi[i+1]-phi[i])](images/SOLPEN9.gif) , respectively and hence
, respectively and hence
| > |
Gamma1[i]:=kappa*(phi[i+1]-2*phi[i]+phi[i-1]);
|
![Gamma1[i] := kappa*(phi[i+1]-2*phi[i]+phi[i-1])](images/SOLPEN10.gif)
The gravity angular moment can be expressed as
| > |
Gamma2[i]:=-M*d*g*sin(phi[i]);
|
![Gamma2[i] := -M*d*g*sin(phi[i])](images/fragment1.gif)
where
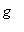 is the gravity constant.
is the gravity constant.
In view of the expressions for
![Gamma1[i]](images/fragment3.gif) and
and
![Gamma2[i]](images/fragment4.gif) , the equations of motion can be rewritten as
, the equations of motion can be rewritten as
| > |
J*diff(phi[i](t),t$2)=kappa*(phi[i+1](t)-2*phi[i](t)+phi[i-1](t))-M*d*g*sin(phi[i](t));
|
,`$`(t,2)) = kappa*(phi[i+1](t)-2*phi[i](t)+phi[i-1](t))-M*d*g*sin(phi[i](t))](images/fragment5.gif)
The above set of equations of motion transforms in the continuous limit to the following partial differential equation
| > |
J*diff(phi(x,t),t$2)=Kappa*diff(phi(x,t),x$2)-K[G]*sin(phi(x,t));
|
![J*diff(phi(x,t),`$`(t,2)) = Kappa*diff(phi(x,t),`$`(x,2))-K[G]*sin(phi(x,t))](images/fragment6.gif)
where
![K[G] = Md*g](images/fragment7.gif) , K=
, K=
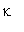 h
^2.
h
^2.
In the new spatial and time variables,
![X = x*sqrt(K[G]/Kappa)](images/SOLPEN20.gif) ,
,
![T = t*sqrt(K[G]/J)](images/SOLPEN21.gif) , the last equation obtains the standard form of the sine-Gordon equation
, the last equation obtains the standard form of the sine-Gordon equation
| > |
diff(phi(X,T),T$2)-diff(phi(X,T),X$2)+sin(phi(X,T))=0;
|
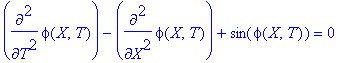
One can see that the system of coupled pendulums is described by the discrete analog to the sine-Gordon equation. In the following, we will demonstrate some of the solutions to the sine-Gordon equation, using the model described above.
Pendulum Model
Warning, the names arrow and changecoords have been redefined
Procedure "pendulum" visualizes, in the frame of pendulum model, the solutions to the sine-Gordon equation obtained with the use of Maple V.
Input parameters:
N_Sol - N-soliton sine-Gordon solution,
name - name of the solution,
L0, L1 - space domain for visualization,
T0, T1 - time domain,
nt - number of snapshots,
nx - number of pendulums in the system,
orient - point of view on the system.
| > |
pendulum:=proc(N_Sol,name,L0,L1,T0,T1,nt,nx,orient)
|
| > |
local ndx,nxx,dx,radius,dt,bases_line,j,dd,
i,theta,cos_u,sin_u,j1,lines,seq_lines,sol_line,seq_sol_line,b,diamonds,seq_diamonds,L,T:
|
| > |
bases_line:=line([0,0,0],[L,0,0],color=black,thickness=1);
|
| > |
for j from 0 to nxx+1 do
|
| > |
theta:=evalf(Re(N_Sol(L0+dd[j],T0+i*dt)-Pi/2));
|
| > |
cos_u[j]:=evalf(radius*cos(theta));
|
| > |
sin_u[j]:=evalf(radius*sin(theta));
|
| > |
lines[j]:=line([dd[j1],0,0],[dd[j1],cos_u[j1],sin_u[j1]],color=blue,thickness=1);
|
| > |
diamonds[j]:=point([dd[j1],cos_u[j1],sin_u[j1]],color=black,symbol=diamond):
|
| > |
seq_lines:=seq(lines[j],j=1..nx):
|
| > |
seq_diamonds:=seq(diamonds[j],j=1..nx):
|
| > |
for j from 1 to nxx-1 do
|
| > |
sol_line[j]:=line([dd[j],cos_u[j],sin_u[j]],[dd[j+1],cos_u[j+1],sin_u[j+1]],thickness=2);
|
| > |
seq_sol_line:=seq(sol_line[j],j=1..nxx-1):
|
| > |
b[i]:=display([seq_lines,seq_diamonds,seq_sol_line,bases_line], color=red):
|
| > |
display(seq(b[i],i=0..nt), insequence=true,axes=framed,title=name,scaling=unconstrained,orientation=orient);
|
Soliton Solutions
Hierarchy of sine-Gordon multi-soliton solutions can be obtained by means of Backlund transformations. Procedure "Backlund" realizes the algorithm of Backlund transformation in Maple V.
Input parameters:
a1, a2 - parameters of transformation,
phi0 - (N-2)-soliton solution,
phi1, phi2 - two (N-1)-soliton solutions.
The outcome of this procedure is the N-soliton solution.
| > |
Backlund := proc (a1,a2,phi0,phi1,phi2) RETURN(phi0+4*arctan(((a1+a2)*tan((phi1-phi2)/4))/(a1-a2))) end;
|
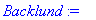
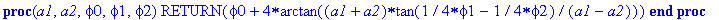
Procedure "Soliton" builds a single-soliton solution.
Input parameters:
x, t - space and time coordinates,
a - parameter of transformation,
x_0 - initial position.
| > |
Soliton := proc (x,t,a,x_0)
local xi,tau:
xi:=(x-x_0+t)/2;
tau:=(x-x_0-t)/2;
RETURN(4*arctan(exp(a*xi+tau/a))) end;
|
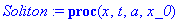
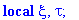
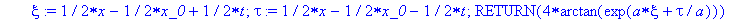

Procedure "TwoSoliton" builds the two-soliton solutions.
Input parameters:
x, t - space and time coordinates,
a1, a2 - parameters of transformation,
x_1, x_2 - initial positions.
| > |
TwoSoliton := proc (x,t,a1,x_1,a2,x_2)
local phi0,phi1,phi2:
phi0[0]:=(x,t)->0;
phi1[1]:=(x,t)->Soliton(x,t,a1,x_1);
phi2[1]:=(x,t)->Soliton(x,t,a2,x_2);
phi1[2]:=(x,t)->Backlund(a1,a2,phi0[0](x,t),phi1[1](x,t),phi2[1](x,t));
RETURN(phi1[2](x,t)) end;
|
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN29.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN30.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN31.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN32.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN33.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN34.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN35.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SOLPEN36.gif)
Procedure "ThreeSoliton" builds the three-soliton solutions.
Input parameters:
x, t - space and time coordinates,
a1, a2, a3 - parameters of transformation,
x_1, x_2, x_3 - initial positions.
| > |
ThreeSoliton := proc (x,t,a1,x_1,a2,x_2,a3,x_3)
local phi,phi1,phi2,phi3 :
phi2[1]:=(x,t)->Soliton(x,t,a2,x_2);
phi1[2]:=(x,t)->TwoSoliton(x,t,a1,x_1,a2,x_2);
phi2[2]:=(x,t)->TwoSoliton(x,t,a2,x_2,a3,x_3);
phi1[3]:=(x,t)->Backlund(a3,a1,phi2[1](x,t),phi2[2](x,t),phi1[2](x,t));
RETURN(Re(phi1[3](x,t))) end;
|
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN37.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN38.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN39.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN40.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN41.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN42.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN43.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SOLPEN44.gif)
One-Soliton Solutions
Kink
| > |
v[K]:=0.1: # velocity of the Kink
|
| > |
x_K:=-4*sqrt(1-v[K]^2): # initial state
|
| > |
a:=sqrt((1-v[K])/(1+v[K])): # parameter of transformation
|
| > |
L:=40*sqrt(1-v[K]^2): T:=(L-2*x_K)/v[K]:
|
| > |
K:=(x,t)->Soliton(x,t,a,x_K):
|
| > |
pendulum(K,"Kink",0,L,0,T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN45.gif)
In the frame of the pendulum model the kink is the solitary wave of counterclockwise rotation of pendulums through the angle
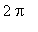 .
.
AntiKink
| > |
v[AK]:=0.1: # velocity of the AntiKink
|
| > |
x_AK:=-4*sqrt(1-v[AK]^2): # initial state
|
| > |
a:=-sqrt((1-v[AK])/(1+v[AK])): # parameter of transformation
|
| > |
L:=40*sqrt(1-v[AK]^2): T:=(L-2*x_AK)/v[AK]:
|
| > |
AK:=(x,t)->Soliton(x,t,a,x_AK):
|
| > |
pendulum(AK,"AntiKink",0,L,0,T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN47.gif)
Antikink is the solitary wave of clockwise rotation of pendulums through the angle
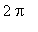 .
.
Two-Soliton Solutions
Kink-Kink Collision
| > |
v[K_K]:=0.2: # velocity of the Kink-Kink
|
| > |
x_K_K:=0: # initial state
|
| > |
a[1]:=sqrt((1-v[K_K])/(1+v[K_K])): # parameters of
|
| > |
a[2]:=-sqrt((1+v[K_K])/(1-v[K_K])): # transformation
|
| > |
L:=10/sqrt(1-v[K_K]^2): T:=L/v[K_K]:
|
| > |
K_K:=(x,t)->TwoSoliton(x,t,a[1],x_K_K,a[2],x_K_K):
|
| > |
pendulum(K_K,"Kink-Kink Collison",-3*L,3*L,-4*T,4*T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN49.gif)
In the frame of the model it is seen that the kinks do not reject each other but pass through each other keeping the direction of pendulum rotation.
Kink-AntiKink Collision
| > |
v[K_AK]:=0.2: # velocity of the Kink-AntiKink
|
| > |
x_K_AK:=0: # initial state
|
| > |
a[1]:=sqrt((1-v[K_AK])/(1+v[K_AK])): # parameters of
|
| > |
a[2]:=sqrt((1+v[K_AK])/(1-v[K_AK])): # transformation
|
| > |
L:=10/sqrt(1-v[K_AK]^2): T:=L/v[K_AK]:
|
| > |
K_AK:=(x,t)->TwoSoliton(x,t,a[1],x_K_AK,a[2],x_K_AK):
|
| > |
pendulum(K_AK,"Kink-AntiKink Collision",-3*L,3*L,-4*T,4*T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN50.gif)
Kink and antikink also pass through each other without any changes.
Breather Solutions
Standing Breather
| > |
v[B]:=0: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
L:=evalf(4*arctan(eta/omega)):
|
| > |
B:=(x,t)->TwoSoliton(x,t,a[1],x_B,a[2],x_B):
|
| > |
pendulum(B,"Standing Breather",-2*L,2*L,-T,T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN51.gif)
Breather is a kind of two-soliton solution, with kink and antikink coupled in an oscillatory system. Oscillations take place in a localized region so that the energy of the breather does not spread with time along the chain.
Large amplitude Breather
| > |
v[B]:=0.2: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
L:=evalf(T*abs(v[B])/(sqrt(1-v[B]^2))):
|
| > |
B:=(x,t)->Re(TwoSoliton(x,t,a[1],x_B,a[2],x_B)):
|
| > |
pendulum(B,"Large amplitude Breather",0,0.9*L,0,T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN52.gif)
Breather can propagate with a constant velocity as a localized oscillatory excitation.
Small amplitude Breather
| > |
v[B]:=0.85: # velocity of the Breather
|
| > |
omega:=0.99: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
T:=evalf(2*2*Pi/omega):
|
| > |
L:=evalf(T*abs(v[B])/(sqrt(1-v[B]^2))):
|
| > |
B:=(x,t)->Re(TwoSoliton(x,t,a[1],x_B,a[2],x_B)):
|
| > |
pendulum(B,"Small amplitude Breather",-2*L,2*L,-4*T,4*T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN53.gif)
Small amplitude breather looks quite exotically.
Three-Soliton Solutions
Standing Kink and Moving Breather collision
| > |
v[K]:=0: # velocity of the Kink
|
| > |
v[B]:=0.5: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=sqrt((1-v[K])/(1+v[K])): # transformation
|
| > |
L:=evalf(T*abs(v[B])/(sqrt(1-v[B]^2))):
|
| > |
x_K:=L/2: # initial state of the Kink
|
| > |
x_B:=0: # initial state of the Breather
|
| > |
K_B:=(x,t)->ThreeSoliton(x,t,a[1],x_B,a[2],x_K,a[3],x_B):
|
| > |
pendulum(K_B,"Standing Kink and Moving Breather collision",-0.5*L,1.5*L,-T,2*T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN54.gif)
This figure illustrates the collision of a moving breather with a standing kink. The velocities and shapes of solitons do not change in the collision. The only result of the collision is the phase shift of solitons. The shift of the kink position after the collision is clearly seen.
Standing Breather and Moving Kink collision
| > |
v[K]:=0.5: # velocity of the Kink
|
| > |
v[B]:=0: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=sqrt((1-v[K])/(1+v[K])): # transformation
|
| > |
x_K:=-4*sqrt(1-v[K]^2): # initial state of the Kink
|
| > |
x_B:=L/2: # initial state of the Breather
|
| > |
K_B:=(x,t)->ThreeSoliton(x,t,a[1],x_B,a[2],x_K,a[3],x_B):
|
| > |
pendulum(K_B,"Standing Breather Moving Kink collision",-L,3*L,-T,2*T,nt,nx,orient);
|
![[Maple Plot]](images/SOLPEN55.gif)
This figure also illustrates the kink-breather collision but here the breather is at rest and the kink moves. The only result of the collision is the phase shift of solitons. In this case, however, the shift of the breather position is not seen so clearly.
Conclusion
With the use of Maple, the Backlund transformation was employed for derivation of several multi-soliton solutions to the sine-Gordon equation. The solutions were visualized for the coupled pendulum model, which has the sine-Gordon equation as the continuous analog.
Disclaimer
While every effort has been made to validate the solutions in this worksheet, Waterloo Maple Inc. and the contributors are not responsible for any errors contained and are not liable for any damages resulting from the use of this material
References
[1] R.K.Dodd, J.C.Eilbeck, J.D.Gibbon, H.C.Morries, Solitons and Nonlinear Wave Equations (Academic Press, London, 1982).
![]() -th pendulum by
-th pendulum by
![]() and the angle velocity by
and the angle velocity by
![]() . Each pendulum experiences the angular moment due to the gravity and the angular moments from the two elastic bonds, which are proportional to the difference in angles of rotation of the coupled pendulums with the coefficient
. Each pendulum experiences the angular moment due to the gravity and the angular moments from the two elastic bonds, which are proportional to the difference in angles of rotation of the coupled pendulums with the coefficient
![]() . Under the assumption that all pendulums have the same moment of inertia, J, the set of equations of motion takes the form Ref. [1]
. Under the assumption that all pendulums have the same moment of inertia, J, the set of equations of motion takes the form Ref. [1]
![]()
![]() is the angular moments from the elastic bonds and
is the angular moments from the elastic bonds and
![]() is the gravity angular moment.
is the gravity angular moment.
![]() and
and
![]() , respectively and hence
, respectively and hence
![]()
![]()
![]() is the gravity constant.
is the gravity constant.
![]() and
and
![]() , the equations of motion can be rewritten as
, the equations of motion can be rewritten as
,`$`(t,2)) = kappa*(phi[i+1](t)-2*phi[i](t)+phi[i-1](t))-M*d*g*sin(phi[i](t))](images/fragment5.gif)
![J*diff(phi(x,t),`$`(t,2)) = Kappa*diff(phi(x,t),`$`(x,2))-K[G]*sin(phi(x,t))](images/fragment6.gif)
![]() , K=
, K=
![]() h
^2.
h
^2.
![X = x*sqrt(K[G]/Kappa)](images/SOLPEN20.gif) ,
,
![T = t*sqrt(K[G]/J)](images/SOLPEN21.gif) , the last equation obtains the standard form of the sine-Gordon equation
, the last equation obtains the standard form of the sine-Gordon equation
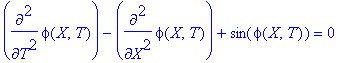
![[Maple Plot]](images/SOLPEN45.gif)
![[Maple Plot]](images/SOLPEN47.gif)
![[Maple Plot]](images/SOLPEN49.gif)
![[Maple Plot]](images/SOLPEN50.gif)
![[Maple Plot]](images/SOLPEN51.gif)
![[Maple Plot]](images/SOLPEN52.gif)
![[Maple Plot]](images/SOLPEN53.gif)
![[Maple Plot]](images/SOLPEN54.gif)
![[Maple Plot]](images/SOLPEN55.gif)