Sine
-Gordon Solitons and Soliton Collisions
by
Andrey E. Miroshnichenko, andrey.miroshnichenko@anu.edu.au,
Aleksey A. Vasiliev, aleksey.vasiliev@tversu.ru,
Sergey V. Dmitriev, sergey@iis.u-tokyo.ac.jp
NOTE: This worksheet demonstrates the use of Maple for obtaining multi-soliton solutions to the sine-Gordon equation, 2D-animation and 3D graphics for representation of the soliton collisions.
Introduction
The localized excitations propagating in a system with constant velocity and colliding with each other without change in their shapes are called solitons. During the collision of solitons the solution cannot be represented as a linear combination of two soliton solutions but after the collision solitons recover their shapes and the only result of collision is a phase shift.
In the worksheet we present the sine-Gordon solitons and their collisions.
The sine-Gordon equation
| > |
diff(phi(x,t),t$2)-diff(phi(x,t),x$2)+sin(phi(x,t))=0;
|
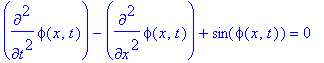
plays an important role in many branches of physics. It provides one of the simplest models of the unified field theory, can be found in the theory of dislocations in metals, in the theory of Josephson junctions and so on. It can be used also in interpreting certain biological processes like DNA dynamics.
Backlund Transformations and Nonlinear Superposition Principle
In the last century a Sweden mathematician Backlund, considering the geometry of surfaces with constant negative curvature, showed a way to obtain the hierarchy of sine-Gordon solutions when a new solution can be build on the bases of known solutions. The transformation, as applied to the sine-Gordon equation, has the form Ref. [1]
| > |
Backl_Trans:={diff((phi(xi,tau)+psi(xi,tau))/2,xi)=a*sin((phi(xi,tau)-psi(xi,tau))/2), diff((phi(xi,tau)-psi(xi,tau))/2,tau)=(1/a)*sin((phi(xi,tau)+psi(xi,tau))/2)};
|
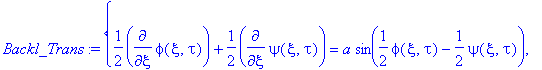
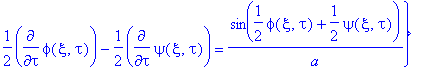
where
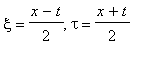 ,
,
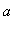 - transformation parameter,
- transformation parameter,
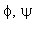 - solutions of the equation
- solutions of the equation
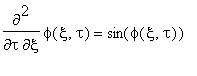 .
.
Assuming that the diagram for the construction of the solutions
![[Maple OLE 2.0 Object]](images/SGe_solitons8.gif)
is commutative, one can eliminate the partial derivatives and find the analytical expression of the Backlund transformations
| > |
phi[n+1]:=phi[n-1]+4*arctan(((a[1]+a[2])/(a[1]-a[2]))*(tan((phi1[n]-phi2[n])/4)));
|
![phi[n+1] := phi[n-1]+4*arctan((a[1]+a[2])*tan(1/4*phi1[n]-1/4*phi2[n])/(a[1]-a[2]))](images/SGe_solitons9.gif)
where
![a[1]](images/SGe_solitons10.gif) ,
,
![a[2]](images/SGe_solitons11.gif) - are the parameters of transformation,
- are the parameters of transformation,
![phi[n]](images/SGe_solitons12.gif) is the n-parametric solution.
is the n-parametric solution.
This formula gives a way to build the multi-soliton solutions.
Procedure "Backlund" realizes the algorithm of Backlund transformation in Maple V.
| > |
Backlund := proc (a1,a2,phi0,phi1,phi2) RETURN(phi0+4*arctan(((a1+a2)*tan((phi1-phi2)/4))/(a1-a2))) end;
|
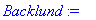
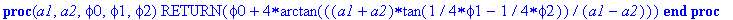
One-Soliton Solutions
Obviously, the sine-Gordon equation has a trivial solution
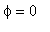 . Substituting the trivial solution into the system "Backl_Trans", one obtains the one-soliton solutions Kink and Antikink.
. Substituting the trivial solution into the system "Backl_Trans", one obtains the one-soliton solutions Kink and Antikink.
| > |
Soliton := proc (x,t,a,x_0)
local xi,tau:
xi:=(x-x_0+t)/2;
tau:=(x-x_0-t)/2;
RETURN(4*arctan(exp(a*xi+tau/a))) end;
|
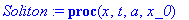
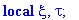
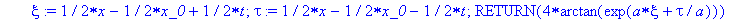

where
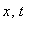 - space and time coordinates,
- space and time coordinates,
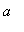 - parameter of transformation for Kink (Antikink),
- parameter of transformation for Kink (Antikink),
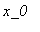 - initial position of Kink (Antikink).
- initial position of Kink (Antikink).
Kink
Warning, the name changecoords has been redefined
| > |
v[K]:=0.1: # velocity of the Kink
|
| > |
x_K:=-4*sqrt(1-v[K]^2): # initial state of the Kink
|
| > |
a:=sqrt((1-v[K])/(1+v[K])): # parameter of transformation
|
| > |
L:=40*sqrt(1-v[K]^2): T:=(L-2*x_K)/v[K]:
|
| > |
K:=(x,t)->Soliton(x,t,a,x_K):
|
| > |
animate(K(x,t),x=0..L,t=0..T,title="Kink",color=red,view=[0..L,-1..2*Pi+1]);
|
![[Maple Plot]](images/SGe_solitons23.gif)
Kink is the transition from one stationary solution,
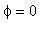 , to another,
, to another,
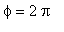 .
.
AntiKink
| > |
v[AK]:=0.1: # velocity of the AntiKink
|
| > |
x_AK:=-4*sqrt(1-v[AK]^2): # initial state of the AntiKink
|
| > |
a:=-sqrt((1-v[AK])/(1+v[AK])): # parameter of transformation
|
| > |
L:=40*sqrt(1-v[AK]^2): T:=(L-2*x_AK)/v[AK]:
|
| > |
AK:=(x,t)->Soliton(x,t,a,x_AK):
|
| > |
animate(AK(x,t),x=0..L,t=0..T,title="AntiKink",color=red,view=[0..L,-1..2*Pi+1]);
|
![[Maple Plot]](images/SGe_solitons26.gif)
Antikink, in contrast to the kink, is the transition from the solution
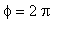 to
to
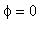 .
.
Two-Solitons Solutions
By applying the Backlund transformation to the trivial solution and one-soliton solution, the two-soliton solutions can be obtained.
| > |
TwoSoliton := proc (x,t,a1,x_1,a2,x_2)
local phi0,phi1,phi2:
phi0[0]:=(x,t)->0;
phi1[1]:=(x,t)->Soliton(x,t,a1,x_1);
phi2[1]:=(x,t)->Soliton(x,t,a2,x_2);
phi1[2]:=(x,t)->Backlund(a1,a2,phi0[0](x,t),phi1[1](x,t),phi2[1](x,t));
RETURN(phi1[2](x,t)) end;
|
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons29.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons30.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons31.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons32.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons33.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons34.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons35.gif)
![TwoSoliton := proc (x, t, a1, x_1, a2, x_2) local phi0, phi1, phi2; phi0[0] := 0; phi1[1] := proc (x, t) options operator, arrow; Soliton(x,t,a1,x_1) end proc; phi2[1] := proc (x, t) options operator, ...](images/SGe_solitons36.gif)
where
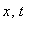 - space and time coordinates,
- space and time coordinates,
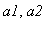 - parameters of transformation,
- parameters of transformation,
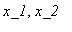 - initial positions.
- initial positions.
Examples of two-soliton solutions and two-soliton collisions:
Kink-Kink Collision
| > |
v[K_K]:=0.2: # velocity of the Kink-Kink
|
| > |
x_K_K:=0: # initial state of the Kink-Kink
|
| > |
a[1]:=-sqrt((1-v[K_K])/(1+v[K_K])): # parameters of
|
| > |
a[2]:=sqrt((1+v[K_K])/(1-v[K_K])): # transformation
|
| > |
L:=10/sqrt(1-v[K_K]^2): T:=L/v[K_K]:
|
| > |
K_K:=(x,t)->TwoSoliton(x,t,a[1],x_K_K,a[2],x_K_K):
|
| > |
animate(K_K(x,t),x=-3*L..3*L,t=-4*T..4*T,title="Kink-Kink Collison",color=red,view=[-3*L..3*L,-2*Pi-1..2*Pi+1]);
|
![[Maple Plot]](images/SGe_solitons40.gif)
Before the collision, Kinks move toward each other with equal velocities. It seems that in the collision they repel each other, however, they actually pass through each other without change in their velocities.
Kink-AntiKink Collision
| > |
v[K_AK]:=0.2: # velocity of the Kink-AntiKink
|
| > |
x_K_AK:=0: # initial state of the Kink-AntiKink
|
| > |
a[1]:=sqrt((1-v[K_AK])/(1+v[K_AK])): # parameters of
|
| > |
a[2]:=sqrt((1+v[K_AK])/(1-v[K_AK])): # transformation
|
| > |
L:=10/sqrt(1-v[K_AK]^2): T:=L/v[K_AK]:
|
| > |
K_AK:=(x,t)->TwoSoliton(x,t,a[1],x_K_AK,a[2],x_K_AK):
|
| > |
animate(K_AK(x,t),x=-3*L..3*L,t=-2*T..2*T,title="Kink-AntiKink Collision",color=red,view=[-3*L..3*L,-2*Pi-1..2*Pi+1]);
|
![[Maple Plot]](images/SGe_solitons41.gif)
Before the collision, Kink and Antikink move toward each other with equal velocities. After the collision they move away with the same velocities but in the neighboring level.
Breather
Another two-soliton solution is the Breather. Breather is an oscillatory localized excitation, which is the Kink and Antikink bound together. Kink and Antikink have no enough energy to overcome their mutual attraction and that is why they make the oscillatory system.
In the following the examples of Breather solutions are given.
Standing Breather
| > |
v[B]:=0: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
T:=2*Pi/omega: L:=4*arctan(eta/omega):
|
| > |
B:=(x,t)->TwoSoliton(x,t,a[1],x_B,a[2],x_B):
|
| > |
animate(B(x,t),x=-2*L..2*L,t=-T..T,title="Standing Breather",color=red,view=[-2*L..2*L,-L-1..L+1],frames=25);
|
![[Maple Plot]](images/SGe_solitons42.gif)
Large amplitude Breather
| > |
v[B]:=0.2: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
T:=2*evalf(2*2*Pi/omega): L:=0.7*evalf(T*abs(v[B])/(sqrt(1-v[B]^2))):
|
| > |
x_B:=-0.5*L: # initial state
|
| > |
B:=(x,t)->Re(TwoSoliton(x,t,a[1],x_B,a[2],x_B)):
|
| > |
animate(B(x,t),x=0..L,t=0..T,title="Large amplitude Breather",color=red);
|
![[Maple Plot]](images/SGe_solitons43.gif)
Moving Breather
| > |
v[B]:=0.85: # velocity of the Breather
|
| > |
omega:=0.85: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
T:=2*2*Pi/omega: L:=T*abs(v[B])/(sqrt(1-v[B]^2)):
|
| > |
B:=(x,t)->Re(TwoSoliton(x,t,a[1],x_B,a[2],x_B)):
|
| > |
animate(B(x,t),x=-2*L..2*L,t=-3.5*T..3.5*T,title="Moving Breather",color=red,view=[-1.5*L..1.5*L,-2.9..2.9],numpoints=260, frames=50);
|
![[Maple Plot]](images/SGe_solitons44.gif)
Small amplitude Breather
| > |
v[B]:=0.85: # velocity of the Breather
|
| > |
omega:=0.99: # frequency of the Breather
|
| > |
x_B:=0: # initial state
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=R*(eta-I*omega): # transformation
|
| > |
T:=2*2*Pi/omega: L:=T*abs(v[B])/(sqrt(1-v[B]^2)):
|
| > |
B:=(x,t)->Re(TwoSoliton(x,t,a[1],x_B,a[2],x_B)):
|
| > |
animate(B(x,t),x=-2*L..2*L,t=-3.5*T..3.5*T,title="Small amplitude Breather",color=red,view=[-1.5*L..1.5*L,-0.9..0.9],numpoints=260, frames=50);
|
![[Maple Plot]](images/SGe_solitons45.gif)
Small amplitude Breather looks exotically but its envelope has the form of large amplitude Breather.
Three-Soliton Solutions
The three-soliton solutions can be obtained according to the diagram called "soliton ladder",
![[Maple OLE 2.0 Object]](images/SGe_solitons46.gif)
which is realized in the following procedure
| > |
ThreeSoliton := proc (x,t,a1,x_1,a2,x_2,a3,x_3)
local phi,phi1,phi2,phi3 :
phi2[1]:=(x,t)->Soliton(x,t,a2,x_2);
phi1[2]:=(x,t)->TwoSoliton(x,t,a1,x_1,a2,x_2);
phi2[2]:=(x,t)->TwoSoliton(x,t,a2,x_2,a3,x_3);
phi1[3]:=(x,t)->Backlund(a3,a1,phi2[1](x,t),phi2[2](x,t),phi1[2](x,t));
RETURN(Re(phi1[3](x,t))) end;
|
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons47.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons48.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons49.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons50.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons51.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons52.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons53.gif)
![ThreeSoliton := proc (x, t, a1, x_1, a2, x_2, a3, x_3) local phi, phi1, phi2, phi3; phi2[1] := proc (x, t) options operator, arrow; Soliton(x,t,a2,x_2) end proc; phi1[2] := proc (x, t) options operator...](images/SGe_solitons54.gif)
where
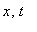 - space and time coordinates,
- space and time coordinates,
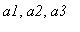 - parameters of transformation,
- parameters of transformation,
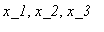 - initial positions.
- initial positions.
This solution describes a wide spectrum of the three-soliton solutions: Kink-Antikink-Kink, Antikink-Kink-Antikink, Kink-Breather and so on.
Let us demonstrate the derivation and graphical representation of the Kink-Breather collision.
Standing Kink and Moving Breather collision
We input parameters and, with the use of the procedure, build the Kink-Breather solution with the Kink standing (
![v[K] = 0](images/SGe_solitons58.gif) ) at
) at
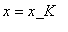 and Breather moving with the frequency
and Breather moving with the frequency
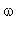 and velocity
and velocity
![v[B]](images/SGe_solitons61.gif) .
.
| > |
v[K]:=0: # velocity of the Kink
|
| > |
v[B]:=0.5: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=sqrt((1-v[K])/(1+v[K])): # transformation
|
| > |
L:=T*abs(v[B])/(sqrt(1-v[B]^2)):
|
| > |
x_K:=L/2: # initial state of the Kink
|
| > |
x_B:=0: # initial state of the Breather
|
| > |
K_B:=(x,t)->Re(ThreeSoliton(x,t,a[1],x_B,a[2],x_K,a[3],x_B)):
|
2D animation of the Kink-Breather interaction.
| > |
ddx:=-2*arctanh(sqrt((1-omega^2)*(1-v[B]^2))):
|
| > |
L0:=line([x_K-ddx,-4], [x_K-ddx,10], color=blue, linestyle=3):
|
| > |
L1:=line([x_K+ddx,-4], [x_K+ddx,10], color=black, linestyle=3):
|
| > |
an_K_B:=animate(K_B(x,t),x=-0.5*L..1.5*L,t=-T..2*T,title="Standing Kink and Moving Breather collision",color=red,numpoints=100):
|
| > |
display([an_K_B,L0,L1]);
|
![[Maple Plot]](images/SGe_solitons62.gif)
The blue line shows the Kink before the collision and the black one after the collision.
Representation of the collision with the use of 3D graphics.
| > |
plot3d(K_B(x,t),x=-0.5*L..1.5*L,t=-T..2*T,title="Standing Kink and Moving Breather collision",orientation=[75,35],grid=[40,40]);
|
![[Maple Plot]](images/SGe_solitons63.gif)
![[Maple Plot]](images/SGe_solitons64.gif)
One can rotate the 3D image in order to observe the process from different points of view.
The presented graphics clearly show that the standing Kink after the collision with the moving Breather do not change its shape and velocity but only shifts to a new position with coordinate
![X_K = x_K+Delta[K]](images/SGe_solitons65.gif) . The shift can be found from the formula
. The shift can be found from the formula
![Delta[K] = -4*arctanh*sqrt((1-omega^2)*(1-v[B]^2))](images/SGe_solitons66.gif) .
.
Standing Kink and Moving Small Amplitude Breather collision
We input parameters and, with the use of the procedure, build the Kink-Breather solution with the Kink standing (
![v[K] = 0](images/SGe_solitons67.gif) ) at
) at
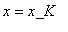 and Breather moving with the frequency
and Breather moving with the frequency
 and velocity
and velocity
![v[B]](images/SGe_solitons70.gif) .
.
| > |
v[K]:=0: # velocity of the Kink
|
| > |
v[B]:=0.85: # velocity of the Breather
|
| > |
omega:=0.99: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=sqrt((1-v[K])/(1+v[K])): # transformation
|
| > |
L:=0.75*T*abs(v[B])/(sqrt(1-v[B]^2)):
|
| > |
x_K:=L/2: # initial state of the Kink
|
| > |
x_B:=0: # initial state of the Breather
|
| > |
K_B:=(x,t)->ThreeSoliton(x,t,a[1],x_B,a[2],x_K,a[3],x_B):
|
2D animation of the Kink-Breather interaction.
| > |
ddx:=-2*arctanh(sqrt((1-omega^2)*(1-v[B]^2))):
|
| > |
L0:=line([x_K-ddx,-4], [x_K-ddx,10], color=blue, linestyle=3):
|
| > |
L1:=line([x_K+ddx,-4], [x_K+ddx,10], color=black, linestyle=3):
|
| > |
an_K_B:=animate(K_B(x,t),x=-0.5*L..1.5*L,t=-T..2*T,title="Standing Kink and Moving Small Amplitude Breather collision",color=red,numpoints=260):
|
| > |
display([an_K_B,L0,L1]);
|
![[Maple Plot]](images/SGe_solitons71.gif)
The blue line shows the Kink before the collision and the black one after the collision.
Representation of the collision with the use of 3D graphics.
| > |
plot3d(K_B(x,t),x=-0.5*L..1.5*L,t=-T..2*T,title="Standing Kink and Moving Breather collision",orientation=[75,35],grid=[40,40]);
|
![[Maple Plot]](images/SGe_solitons72.gif)
![[Maple Plot]](images/SGe_solitons73.gif)
One can rotate the 3D image in order to observe the process from different points of view.
The presented graphics clearly show that the standing Kink after the collision with the moving Breather do not change its shape and velocity but only shifts to a new position with coordinate
![X_K = x_K+Delta[K]](images/SGe_solitons74.gif) . The shift can be found from the formula
. The shift can be found from the formula
![Delta[K] = -4*arctanh*sqrt((1-omega^2)*(1-v[B]^2))](images/SGe_solitons75.gif) .
.
Standing Breather and Moving Kink collision
In this section we present the interaction of standing (
![v[B] = 0](images/SGe_solitons76.gif) ) at
) at
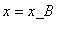 Breather with the Kink moving with the velocity
Breather with the Kink moving with the velocity
![v[K]](images/SGe_solitons78.gif) .
.
| > |
v[K]:=0.5: # velocity of the Kink
|
| > |
v[B]:=0: # velocity of the Breather
|
| > |
omega:=0.154: # frequency of the Breather
|
| > |
R:=sqrt((1-v[B])/(1+v[B])):
|
| > |
a[1]:=R*(eta+I*omega): # parameters of
|
| > |
a[2]:=sqrt((1-v[K])/(1+v[K])): # transformation
|
| > |
x_K:=-4*sqrt(1-v[K]^2): # initial state of the Kink
|
| > |
x_B:=L/2: # initial state of the Breather
|
| > |
K_B:=(x,t)->ThreeSoliton(x,t,a[1],x_B,a[2],x_K,a[3],x_B):
|
2D animation of the Kink-Breather interaction.
| > |
ddx:=-arctanh(sqrt((1-omega^2)*(1-v[K]^2)))/sqrt(1-omega^2):
|
| > |
L0:=line([x_B-ddx,-6], [x_B-ddx,12], color=blue, linestyle=3):
|
| > |
L1:=line([x_B+ddx,-6], [x_B+ddx,12], color=black, linestyle=3):
|
| > |
an_B_K:=animate(K_B(x,t),x=-L..3*L,t=-T..2*T,title="Standing Breather Moving Kink collision",color=red):
|
| > |
display([an_B_K,L0,L1]);
|
![[Maple Plot]](images/SGe_solitons79.gif)
The blue line shows the breather before the collision and the black one after the collision.
3D representation of the collision.
| > |
plot3d(K_B(x,t),x=-L..2*L,t=-T..2*T,title="Standing Breather Moving Kink collision",orientation=[70,45],grid=[40,40]);
|
![[Maple Plot]](images/SGe_solitons80.gif)
![[Maple Plot]](images/SGe_solitons81.gif)
One can rotate the 3D image in order to observe the process from different points of view.
The presented graphics clearly show that the velocity and the oscillation frequency of the standing Breather, after the collision with the moving Kink, are unchanged. The position of the Breather shifts after collision to
![X_B = x_B+Delta[B]](images/SGe_solitons82.gif) . The shift can be found from the formula
. The shift can be found from the formula
![Delta[B] = 2*arctanh*sqrt((1-omega^2)*(1-v[K]^2))/sqrt(1-omega^2)](images/SGe_solitons83.gif) .
.
Conclusion
In the present worksheet, we demonstrated the power of MAPLE deriving the multi-soliton solutions to the sine-Gordon equation with the use of Backlund transformations. We considered both real and complex parameters of transformations. The solutions are given in the form of recursion procedures, which gives an efficient representation of the "soliton ladder" idea. Animation and 3D graphics help to visualize the basic properties of soliton collisions.
Disclaimer
While every effort has been made to validate the solutions in this worksheet, Waterloo Maple Inc. and the contributors are not responsible for any errors contained and are not liable for any damages resulting from the use of this material.
References
[1] R.K.Dodd, J.C.Eilbeck, J.D.Gibbon, H.C.Morries, Solitons and Nonlinear Wave Equations (Academic Press, London, 1982).
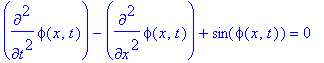
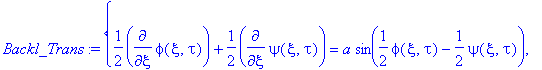
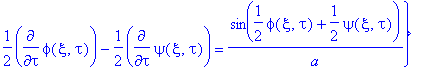
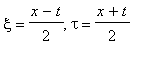 ,
,
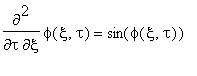 .
.
![[Maple OLE 2.0 Object]](images/SGe_solitons8.gif)
![phi[n+1] := phi[n-1]+4*arctan((a[1]+a[2])*tan(1/4*phi1[n]-1/4*phi2[n])/(a[1]-a[2]))](images/SGe_solitons9.gif)
![[Maple Plot]](images/SGe_solitons23.gif)
![[Maple Plot]](images/SGe_solitons26.gif)
![[Maple Plot]](images/SGe_solitons40.gif)
![[Maple Plot]](images/SGe_solitons41.gif)
![[Maple Plot]](images/SGe_solitons42.gif)
![[Maple Plot]](images/SGe_solitons43.gif)
![[Maple Plot]](images/SGe_solitons44.gif)
![[Maple Plot]](images/SGe_solitons45.gif)
![[Maple OLE 2.0 Object]](images/SGe_solitons46.gif)
![[Maple Plot]](images/SGe_solitons62.gif)
![[Maple Plot]](images/SGe_solitons63.gif)
![[Maple Plot]](images/SGe_solitons64.gif)
![Delta[K] = -4*arctanh*sqrt((1-omega^2)*(1-v[B]^2))](images/SGe_solitons66.gif) .
.
![[Maple Plot]](images/SGe_solitons71.gif)
![[Maple Plot]](images/SGe_solitons72.gif)
![[Maple Plot]](images/SGe_solitons73.gif)
![Delta[K] = -4*arctanh*sqrt((1-omega^2)*(1-v[B]^2))](images/SGe_solitons75.gif) .
.
![[Maple Plot]](images/SGe_solitons79.gif)
![[Maple Plot]](images/SGe_solitons80.gif)
![[Maple Plot]](images/SGe_solitons81.gif)
![Delta[B] = 2*arctanh*sqrt((1-omega^2)*(1-v[K]^2))/sqrt(1-omega^2)](images/SGe_solitons83.gif) .
.