Introduction

The basic properties of solitons, like propagation and interaction without change in their velocity and shape, make it possible to treat them as the robust localized objects. Solitons show their duality, having both the properties of particles and waves. A soliton has the wave nature and finite width but it behaves itself as a particle when interacting with other solitons. That is why the solitons are often spoken of as quasiparticles. It is known that for solitons in a completely integrable system there exist an infinitely large number of conservation laws. For example, not only the energy and momentum but also a characteristic, which can be called "charge", is conserved in the system. There exist several physical interpretations of the sine-Gordon equation, therefore this charge will be called here the topological charge, without specification for a particular model.

Elastic Ribbon Model

Let us twist one end of the elastic ribbon with respect to another through angle 2 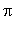. As a result of this operation a twist, which can propagate along the ribbon, will be formed Ref. [1]. The ribbon can be twisted either clockwise or counterclockwise. Therefore, the twist can be regarded as a charged particle and the sign of charge is defined by the direction of twisting.

>

restart:

>	with(plots):

>	with(plottools):

Warning, the name changecoords has been redefined

Warning, the assigned name arrow now has a global binding

Procedure "ribbon" visualizes the solutions to the sine-Gordon equation for the elastic ribbon model.

Input parameters:
N_Sol - N-soliton sine-Gordon solution,
name - name of the solution,
L0, L1 - space domain for visualization,
T0, T1 - time domain,
orient - point of view on the system.

>	ribbon:=proc(N_Sol,name,L0,L1,T0,T1,orient)

>	local nt,ndx,nx,nxx,dx,radius,dt,bases_line,j,dd,i,theta,cos_u,sin_u,j1,arrows,seq_arrows,lines,seq_lines,theta_r,cos_u_r,sin_u_r,polygons,seq_polygons,b,tar,L,T:

>

>	assume(nt,integer);assume(ndx,integer);

>	assume(nx,integer);assume(nxx,integer);

>	nt:=40: ndx:=10:

>	nx:=10: nxx:=nx*ndx:

>	L:=L1-L0: T:=T1-T0:

>	dx:=L/nxx: dt:=T/nt:

>	tar:=L/(7*nx): radius:=L/20:

>

>	bases_line:=line([0,0,0],[L,0,0],color=black );

>	for j from 0 to nxx+1 do

>	dd[j]:=dx*j;

>

od:

>	for i from 0 to nt do

>	for j from 1 to nxx do

>	theta:=N_Sol(L0+dd[j],T0+i*dt)+Pi/2;

>	cos_u[j]:=evalf(radius*cos(theta));

>	sin_u[j]:=evalf(radius*sin(theta));

>

od:

>	for j from 1 to nx do

>	j1:=j*ndx;

>	arrows[j]:=arrow([dd[j1],0,0],[dd[j1],cos_u[j1],sin_u[j1]],tar,3*tar, 0.2,color=blue);

>

od;

>	seq_arrows:=seq(arrows[j],j=1..nx):

>	for j from 1 to nxx-1 do

>	lines[j]:=line([dd[j],cos_u[j],sin_u[j]],[dd[j+1],cos_u[j+1],sin_u[j+1]],color=red,thickness=2);

>

od;

>	seq_lines:=seq(lines[j],j=1..nxx-1):

>	for j from 1 to nxx+1 do

>	theta_r:=N_Sol(L0+dd[j],T0+i*dt);

>	cos_u_r[j]:=evalf(radius*cos(theta_r));

>	sin_u_r[j]:=evalf(radius*sin(theta_r));

>

od;

>	for j from 2 to nxx+1 do

>	polygons[j]:=polygon([[dd[j-1],-cos_u_r[j-1],-sin_u_r[j-1]],[dd[j],-cos_u_r[j],-sin_u_r[j]],[dd[j-1],cos_u_r[j-1],sin_u_r[j-1]],[dd[j],cos_u_r[j],sin_u_r[j]]], color=green); od:

>	seq_polygons:=seq(polygons[j],j=2..nxx+1);

>	b[i]:=display([seq_arrows,seq_lines,bases_line,seq_polygons], color=red):

>

od:

>	display(seq(b[i],i=0..nt), insequence=true,axes=framed,title=name,scaling=unconstrained,orientation=orient);

>

end:

Soliton Solutions

Hierarchy of sine-Gordon multi-soliton solutions can be obtained by means of Backlund transformations Ref. [1]. Procedure "Backlund" realizes the algorithm of Backlund transformation in Maple V.
Input parameters:
a1, a2 - parameters of transformation,
phi0 - (N-2)-soliton solution,
phi1, phi2 - two (N-1)-soliton solutions.
The outcome of this procedure is the N-soliton solution.

>	Backlund := proc (a1,a2,phi0,phi1,phi2) RETURN(phi0+4*arctan(((a1+a2)*tan((phi1-phi2)/4))/(a1-a2))) end;

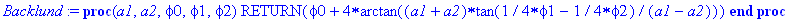
Procedure "Soliton" builds a single-soliton solution.
Input parameters:
x, t - space and time coordinates,
a - parameter of transformation,
x_0 - initial position.

>	Soliton := proc (x,t,a,x_0) local xi,tau: xi:=(x-x_0+t)/2; tau:=(x-x_0-t)/2; RETURN(4*arctan(exp(a*xi+tau/a))) end;

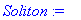
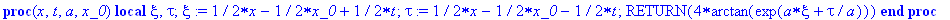
Procedure "TwoSoliton" builds the two-soliton solutions.
Input parameters:
x, t - space and time coordinates,
a1, a2 - parameters of transformation,
x_1, x_2 - initial positions.

>	TwoSoliton := proc (x,t,a1,x_1,a2,x_2) local phi0,phi1,phi2: phi0[0]:=(x,t)->0; phi1[1]:=(x,t)->Soliton(x,t,a1,x_1); phi2[1]:=(x,t)->Soliton(x,t,a2,x_2); phi1[2]:=(x,t)->Backlund(a1,a2,phi0[0](x,t),phi1[1](x,t),phi2[1](x,t)); RETURN(phi1[2](x,t))  end;

Procedure "ThreeSoliton" builds the three-soliton solutions.
Input parameters:
x, t - space and time coordinates,
a1, a2, a3 - parameters of transformation,
x_1, x_2, x_3 - initial positions.

>

ThreeSoliton := proc (x,t,a1,x_1,a2,x_2,a3,x_3) local  phi,phi1,phi2,phi3 : phi2[1]:=(x,t)->Soliton(x,t,a2,x_2); phi1[2]:=(x,t)->TwoSoliton(x,t,a1,x_1,a2,x_2); phi2[2]:=(x,t)->TwoSoliton(x,t,a2,x_2,a3,x_3); phi1[3]:=(x,t)->Backlund(a3,a1,phi2[1](x,t),phi2[2](x,t),phi1[2](x,t)); RETURN(Re(phi1[3](x,t)))  end;

One-Soliton Solutions

Two-Soliton Solutions

Three-Soliton Solutions

In the two last figures, the kink-breather collisions are presented for the cases when one of the quasiparticles moves and another one is at rest. Of course, for these collisions the total charge = , is also conserved. These two solutions, describing kink-breather collisions, are actually identical in the sense that one of them can be transformed to another by means of the Lorentz transformation for an inertial system. All the collisions described above are the elastic collisions or, in other words, there is no energy and momentum exchange between colliding quasiparticles. However, for the discrete sine-Gordon system the collision of more than two solitons can be strongly inelastic even at a very small degree of discreteness. For example, in Ref. [2], the domain of parameters has been given where the transformation of kink-breather solution to the kink-antikink-kink solution becomes possible. This transformation is not forbidden by the charge conservation law because = .

Conclusion

In the present worksheet, with the use of MAPLE, the multi-soliton solutions to the sine-Gordon equation were discussed in the frame of the elastic ribbon model, which allows the consideration of solitons as the charged particles. For the presented animations we tried to choose the parameters in a way to demonstrate, in the clearest form, the charge conservation law.

References

[1] R.K.Dodd, J.C.Eilbeck, J.D.Gibbon, H.C.Morries, Solitons and Nonlinear Wave Equations (Academic Press, London, 1982).

[2] S.V.Dmitriev, T.Shigenari, A.A.Vasiliev, A.E.Miroshnichenko, Effect of  discreteness on a sine-Gordon three-soliton solution // Phys.Lett. A   246 (1998) 129-134.